Quote:
Originally Posted by Carl Copeland
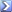
Alexander, as intriguing as the poem and its translation(s) are, I feel they were a red herring in this puzzle (encouraging us to think of it as a word problem and based on multiples of two rather than three), but never mind that. I’m more interested in the solution.
|
Carl, here
https://math.berkeley.edu/~giventh/mirrors.pdf I posted three pictures.
The top one shows that if the angle between two mirrors is random, then the number of mirror images (produced by consecutive reflections in the counterclockwise direction) can be large, potentially infinite in the case when the angle is not a fractional part of 360 degrees but an irrational part of it.
The middle picture shows, in the case of two perpendicular mirrors in 2D, how the light trajectories from the object to the eye can be reconstructed from the straight rays from the three phantom images (color-coded).
The bottom picture adapts the photo that Roger sent to us to the case of three pairwise perpendicular mirrors, and shows one of possible (depending on the position of the observer) positions of the 8 images of
the candle.
As about the red herring: why?
I said from the start that it is a
math, not word challenge.
The typical error one makes is thinking that 2 (or 3) mirrors produce 2 (resp. 3) mirror images - one per mirror.
Any poem consists of words, quatrains, etc., but this one is very unusual if not outright unique: it translates a text into the same language (and likens a translation to a mirror image). Moreover, the poem is translated into English, so that the initial text is reflected in two metaphorical mirrors.
Thus, my hint was fair: these two "mirrors" produce not 2 copies of the original text but 3. And the hint worked for Sarah-Jane!
As a surplus, there comes the fact that the poem refers to an actual mirror (that's how the metaphor is established), and so if you count the overall number of the Moons there, it is 8 - and for exactly the same reason why there are 8 images of an object reflected in three perpendicular mirrors. Namely, the corner of a room is 1/8-th of the whole space (accessible to Alice) and with every mirror reflection, it doubles - just as the number of copies (of the Moon, or quatrain) doubles with every reflection, be it physical or metaphorical.